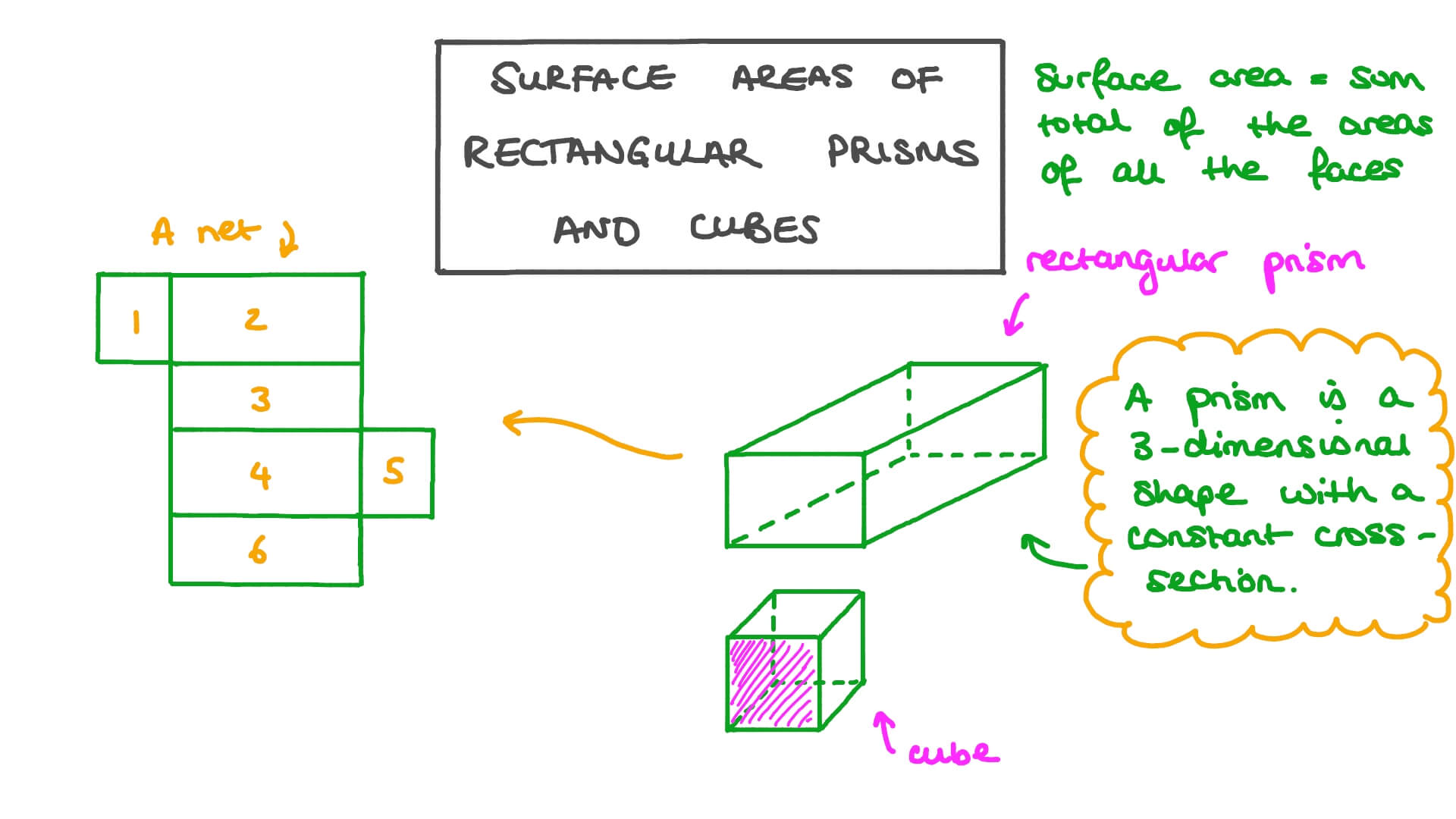
Whether you're a student learning the basics of geometry or a professional applying these concepts in real-world scenarios, this formula is a cornerstone of spatial mathematics. A rectangular prism, also known as a cuboid, is a three-dimensional shape with six rectangular faces. Calculating its surface area involves summing the areas of all these faces, and the formula simplifies this process. This guide will walk you through every aspect of the rectangular prism surface area formula, ensuring you gain a thorough understanding of its applications and significance. The rectangular prism surface area formula isn't just a theoretical concept; it has practical applications in fields like architecture, engineering, packaging, and even art. For instance, architects use it to calculate the amount of material needed to cover a building's exterior, while manufacturers rely on it to determine the packaging requirements for products. By mastering this formula, you'll not only enhance your mathematical skills but also equip yourself with a tool that can solve real-world problems. This article will delve into the formula's components, step-by-step calculations, and tips for avoiding common mistakes. As we explore the rectangular prism surface area formula, you'll discover how it connects to broader mathematical principles and other geometric shapes. We'll also address frequently asked questions, provide practical examples, and offer insights into how this formula can be applied in various contexts. By the end of this guide, you'll have a comprehensive understanding of the formula and the confidence to apply it in both academic and practical settings. Let’s dive into the details and unlock the potential of this fundamental geometric concept.
Table of Contents
- What Is the Rectangular Prism Surface Area Formula?
- How to Calculate the Surface Area of a Rectangular Prism?
- Why Is the Surface Area Formula Important?
- Common Mistakes to Avoid
- Applications in Real Life
- How Does This Formula Relate to Other Shapes?
- Step-by-Step Guide to Solving Problems
- Frequently Asked Questions
What Is the Rectangular Prism Surface Area Formula?
The rectangular prism surface area formula is a mathematical expression used to calculate the total area covered by all six faces of a rectangular prism. The formula is expressed as:
Surface Area = 2lw + 2lh + 2wh
Read also:Julie Barry From Survivor The Ultimate Guide To Her Journey And Life
Here, l represents the length, w represents the width, and h represents the height of the prism. Each term in the formula corresponds to the area of two opposite faces. For example, 2lw calculates the combined area of the front and back faces, 2lh covers the left and right faces, and 2wh accounts for the top and bottom faces.
Why Is This Formula So Effective?
The beauty of the rectangular prism surface area formula lies in its simplicity and versatility. By breaking down the prism into its constituent faces, the formula allows you to compute the total surface area systematically. This approach ensures accuracy and minimizes errors, especially when dealing with complex dimensions. Additionally, the formula is scalable, meaning it works for prisms of any size, from small objects like boxes to large structures like buildings.
Understanding the Components
To fully grasp the formula, it’s important to understand its components:
- Length (l): The longest side of the prism.
- Width (w): The shorter side of the prism’s base.
- Height (h): The vertical dimension of the prism.
Each of these dimensions plays a crucial role in determining the surface area, and any error in measuring them can lead to incorrect results. Therefore, precision is key when applying the formula.
How to Calculate the Surface Area of a Rectangular Prism?
Calculating the surface area of a rectangular prism involves a systematic approach. Let’s break it down step by step:
- Identify the Dimensions: Measure or obtain the length (l), width (w), and height (h) of the prism.
- Apply the Formula: Plug the values into the formula: Surface Area = 2lw + 2lh + 2wh.
- Perform the Calculations: Multiply the dimensions as indicated, then sum the results.
- Double-Check Your Work: Verify each step to ensure accuracy.
For example, consider a rectangular prism with l = 5 cm, w = 3 cm, and h = 4 cm. Using the formula:
Read also:Why Spencer Star Diapers Are The Ultimate Choice For Parents
Surface Area = 2(5 × 3) + 2(5 × 4) + 2(3 × 4)
Surface Area = 30 + 40 + 24 = 94 cm²
What Are Some Practical Examples?
Let’s explore a few real-world scenarios where this calculation is useful:
- Packaging Design: A company designing a cereal box needs to calculate the surface area to determine the amount of cardboard required.
- Painting a Room: An interior designer uses the formula to estimate the amount of paint needed to cover the walls of a rectangular room.
- Construction Projects: Engineers apply the formula to calculate the surface area of concrete slabs or walls.
Why Is the Surface Area Formula Important?
The rectangular prism surface area formula is more than just a mathematical tool; it’s a practical solution for a variety of challenges. Its importance can be seen in both academic and professional settings, as well as in everyday life. For students, mastering this formula builds a strong foundation in geometry and enhances problem-solving skills. For professionals, it serves as a reliable method for making accurate calculations in fields like architecture, manufacturing, and logistics.
What Are the Benefits of Knowing This Formula?
Understanding the rectangular prism surface area formula offers several advantages:
- Efficiency: It simplifies complex calculations, saving time and effort.
- Accuracy: By following a systematic approach, it minimizes the risk of errors.
- Versatility: The formula can be applied to a wide range of objects and scenarios.
Broader Implications
Beyond its immediate applications, the formula also helps develop critical thinking and spatial reasoning skills. These skills are invaluable in fields that require visualization and problem-solving, such as engineering, design, and computer graphics.
Common Mistakes to Avoid
While the rectangular prism surface area formula is straightforward, there are common pitfalls that can lead to incorrect results. Being aware of these mistakes can help you avoid them and ensure accurate calculations.
- Incorrect Dimensions: Using the wrong values for length, width, or height can throw off the entire calculation.
- Forgetting to Double the Areas: Each pair of opposite faces must be accounted for, so forgetting to multiply by 2 is a frequent error.
- Unit Inconsistencies: Mixing different units (e.g., meters and centimeters) can lead to inaccurate results.
How Can You Avoid These Mistakes?
To prevent errors, follow these tips:
- Double-Check Measurements: Always verify the dimensions before plugging them into the formula.
- Use Consistent Units: Ensure all measurements are in the same unit before performing calculations.
- Break Down the Formula: Calculate each term separately to avoid confusion.
Applications in Real Life
The rectangular prism surface area formula finds applications in numerous real-world scenarios. Its versatility makes it an indispensable tool in various industries and everyday situations.
- Architecture: Architects use the formula to calculate the surface area of walls, roofs, and floors.
- Manufacturing: It helps determine the amount of material needed for packaging, such as boxes and cartons.
- Art and Design: Artists and designers apply the formula to create three-dimensional models and sculptures.
Why Is It Relevant in Everyday Life?
Even outside professional settings, the formula can be useful. For instance, if you’re painting a room or wrapping a gift, knowing how to calculate the surface area ensures you have enough material to complete the task without waste.
How Does This Formula Relate to Other Shapes?
The rectangular prism surface area formula is part of a broader family of geometric formulas used to calculate the surface areas of different shapes. Understanding its relationship to other formulas can deepen your knowledge of geometry.
- Cubes: A cube is a special case of a rectangular prism where all sides are equal. The formula simplifies to Surface Area = 6s², where s is the side length.
- Cylinders: The surface area of a cylinder is calculated using a different formula: Surface Area = 2πr² + 2πrh.
- Spheres: For a sphere, the formula is Surface Area = 4πr².
What Are the Key Differences?
While the rectangular prism formula focuses on summing the areas of rectangular faces, other formulas account for curved surfaces or circular bases. This distinction highlights the unique properties of each shape and the importance of selecting the correct formula for the task at hand.
Step-by-Step Guide to Solving Problems
Solving problems involving the rectangular prism surface area formula requires a structured approach. Here’s a step-by-step guide to help you tackle any problem with confidence:
- Read the Problem Carefully: Identify the given dimensions and what is being asked.
- Write Down the Formula: Always start by writing the formula to ensure clarity.
- Substitute the Values: Plug the given dimensions into the formula.
- Perform the Calculations: Multiply and add the terms systematically.
- Verify Your Answer: Double-check your work to ensure accuracy.
What If the Dimensions Are Missing?
If the problem doesn’t provide all the dimensions, you may need to use additional information or formulas to find the missing values. For example, if the volume is given, you can use the volume formula (Volume = l × w × h) to solve for one of the dimensions.
Frequently Asked Questions
What Is the Difference Between Surface Area and Volume?
Surface area refers to the total area covered by the outer surfaces of a three-dimensional object, while volume measures the space enclosed within the object. The rectangular prism surface area formula calculates the former, while the volume formula calculates the latter.
Can the Formula Be Used for Other Shapes?
The rectangular prism surface area formula is specific to rectangular prisms. However, similar principles can be applied to other shapes, provided you use the appropriate formula for that shape.
Why Is the Formula Multiplied by 2?
The formula multiplies each term by 2 because a rectangular prism has pairs of opposite faces. Each pair contributes equally to the total surface area, so doubling ensures all faces are accounted for.
Conclusion